Winkelfunktionen beim rechtwinkeligen Dreieck - Grundlagen

AM-Übersicht

Zimmerer-Seite

Benennung der Elemente

Dreiecke besitzen 3 Seiten und 3 eingeschlossene Winkel. Die Hypotenuse, die längste Seite, ist immer gegenüber dem rechten Winkel, dem größten Winkel. Die zwei kürzeren Seiten sind die Katheten. Nun kommt es darauf an welchen Winkel man betrachtet. Die diesem Winkel gegenüberliegende Seite heißt Gegenkathete. Die an den betrachteten Winkel angrenzende Seite heißt Ankathete. Der betrachtete Winkel wird mit dem griechischen Buchstaben α "alpha" bezeichnet. Abkürzungen:   Hypotenuse . . . H Gegenkathete . . . GK Ankathete . . . AK Übung Elemente zuordnen

Formeln

Sind bei rechtwinkeligen Dreiecken 2 Elemente gegeben, so können alle anderen Elemente ausgerechnet werden.

Grundformel	Ableitungen

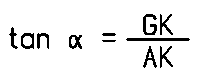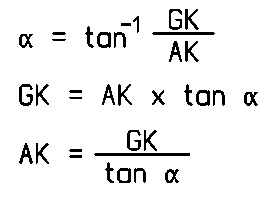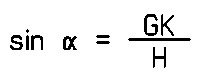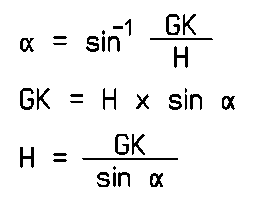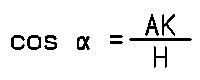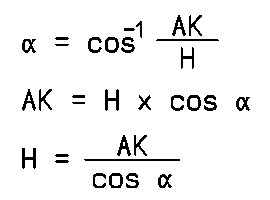Die richtigen Funktion auswählen

1. Welche Seite oder welcher Winkel soll errechnet werden?
2. Man stellt fest welche der Dreieckselemente gegeben sind. (Aus zwei Seiten kann ein Winkel, oder aus einer Seite und einem Winkel eine weitere Seite errechnet werden.)
3. Nun wählt man jene Winkelfunktion, in der alle 3 Elemente enthalten sind.
4. Im nächsten Schritt wird die Winkelfunktion umgeformt, oder die entsprechende Ableitung verwendet.

Übungen

die richtige Funktion wählen

die richtige Formel wählen

Größen abschätzen

Einfache Rechenbeispiele:  Bsp.1 Bsp.2 Bsp.3 Bsp.4		PDF-Übungsblatt Grundlagen 1 Grundlagen 3
Aktive Rechenbeispiele:  Bsp.1 Bsp.2 Bsp.3 Bsp.4 Bsp.5 Bsp.6

Übungsblätter im PDF-Format

Schülerangaben	Blatt 1	Blatt 2	Blatt 3, 4	Blatt 5, 6	Blatt 7, 8	Blatt 9, 10	Blatt 11, 12
Lösungen	Blatt 1 und 2		Blatt 3, 4	Blatt 5, 6	Blatt 7, 8	Blatt 9, 10	Blatt 11, 12

Weitere einfache Beispiele:	Dachgeometrie Satteldach
	Berechnungen am Normalprofil
	Dachgeometrie Walmdach
	Dachgeometrie Krüppelwalmdach

Übersicht Winkelfunktionen, rechtwinkelig und schiefwinkelige Dreiecke.

Sinus-, Cosinussatz

Zum Seitenanfang

Zimmerer-Seite